링크)
논문 다운로드
해당 논문 데이터
먼저 NeRF에 대하여 본격적으로 들어가기 전 제목에 있는 View Synthesis에 대해 파악하고 들어가는 것이 좋다고 생각합니다.
View는 ‘시야’, Synthesis는 ‘합성’이라는 사전적 의미를 가지고 있습니다. 이로 미루어 보았을 때, 시야를 합성한다는 것은 사진에 실제로 보이지 않더라도 우리가 사물의 특정 시점에서의 모습을 알고 있다면 예측을 통해 이를 3D로 바꿀 수 있다는 것입니다.

위 사진을 예로 들어보겠습니다. 사진에서는 두 사람의 모습을 배꼽 정도의 높이에 특정 앵글에서 표현했습니다. 흔히 영화에서 이런 기법이 자주 사용되곤 하죠. 임의의 관찰자의 시점으로 장면을 본 것입니다. 지금은 여배우가 등을 보이고 있지만 제가 만약 똑같은 배꼽 높이에서, 정확히 반대편에서, 관찰자와 배우 같은 간격도 같은 곳에서 여배우의 앞모습을 보려고 한다면 어떻게 될까요?
이 두 사람 주위에 돔 형으로 n대의 카메라가 있다고 가정해 봅시다. 돔형으로 카메라가 존재하는 이유는 이 장면을 다양한 시야에서 바라보기 위해서입니다. 이 카메라들은 하나의 좌표와도 같습니다. 3차원이기에 (x, y, z)로 표현될 것입니다. 아까 제가 말한 앞모습을 구현하기 위해서는 반대편의 배경, 남자의 뒷모습과 여자의 앞모습을 알아야 합니다. 이 일을 돔형 카메라들이 해 줄 것입니다. 굳이 카메라들이 엄청 촘촘하게 배열되어 있지 않아도 됩니다. 어쨌든 이렇게 대략적인 정보를 얻은 후 우리가 얻고자 하는 특정 좌표에서의 이미지를 얻어 봅시다.
위에서 저는 예측이라는 단어를 사용했습니다. 이를 결과에 적용해 보면 정확한 해당 좌표에서의 이미지는 모르더라도 다른 좌표들에서 얻은 이미지를 이용해 해당 좌표에서의 이미지를 예측하여 제공하는 것입니다. 이러한 시도가 수없이 반복된다면 우리는 자연스럽게 엄청난 밀도에서의 이미지들을 얻게 되고 이를 이으면 하나의 continuous 한 3D 이미지가 완성되는 것입니다.
이렇게 구동되는 View Synthesis에서 가장 중요한 문제는 바로 Parellex Effect입니다. 예를 들어 https://www.matthewtancik.com/nerf에 있는 3D 이미지를 보면 “아니 카메라가 좌우로 움직이는 거면 그냥 이미지를 좌우로 shifting 하면 되는 거 아닌가?”라는 의문이 들 수도 있습니다. 그렇게 단순 shifting을 하면 안 되는 이유는 링크 속 이미지를 보시면 아무리 같은 사물이라 할지라도 이미지 상에서 멀리 있는 부분은 카메라가 움직일 때 거의 움직이지 않는 것처럼 보이고 가까운 부분은 조금만 카메라가 가도 많이 움직이는 것처럼 보입니다. 원근법에서 비롯된 현상이라고 볼 수 있겠죠. 이런 Depth와 관련된 문제가 바로 Parellex Effect입니다.
Parellex Effect를 일상생활에서 가장 잘 확인할 수 있는 경우는 밤에 달이 나를 따라오는 것 같다고 느끼는 것과 같습니다. 달이 나를 따라오는 것 같다고 느끼는 이유도 달과 나의 거리가 멀 기 때문에 내가 상하좌우로 움직이는 거리 대비 달은 거의 움직이지 않는 것처럼 보이기 때문입니다. 만약 달과의 거리가 가까웠다면 차를 타고 가다가 달이 지는 것처럼 보이는 경우가 생길 수도 있겠죠?
이제 depth가 중요하다는 것은 알았습니다. 그럼 이제 이 depth를 어떤 방식으로 표현하는지 알아야 합니다. 먼저 pinhole camera model에 대해 알아보겠습니다.
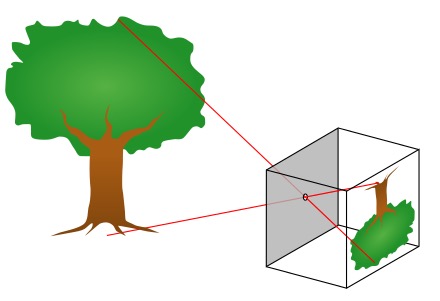
학창 시절 과학 시간에 비슷한 그림을 봤던 기억이 납니다. 저 박스를 카메라라고 가정했을 때, 이 사진은 어떻게 3D사진이 2D로 담기는지를 나타내고 있습니다. 사진을 보면 실제 나무의 크기와 맺힌 상에서의 나무의 크기가 다릅니다. 이를 통해 이 pinhole camera model이 얘기하고 싶은 것은 실제 세상과 카메라를 통해 얻은 이미지와의 관계를 나타내는 것입니다.
여기서 말한 관계를 알기 위해서는 카메라의 정보와 카메라와 대상 간의 거리를 알아야 합니다. 후자의 경우에는 아무리 같은 길이라고 할지라도 카메라 기준으로 거리에 따라 상대적으로 길고 짧아 보일 수 있기 때문입니다. 그리고 카메라의 정보를 알아야 하는 이유는 실제로 몇 미터인지를 알기 위함입니다. 이미지는 기본적으로 픽셀로 이루어져 있기에 얼마만큼의 픽셀로 이루어져 있는지를 파악하면서 실제 세상에서의 길이를 상대적으로 담아낼 수 있게 되는 것입니다.
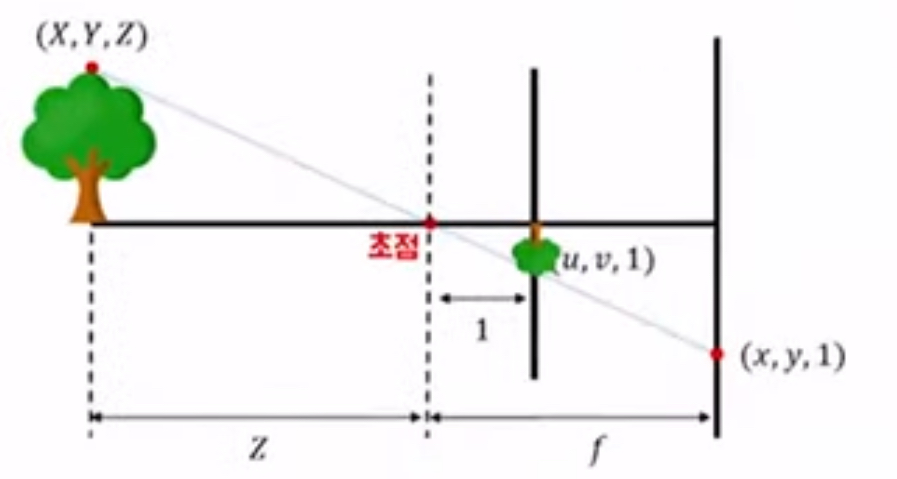
위 이미지를 해석하면 왼쪽에 실제 나무가 있고 초점은 카메라의 위치입니다. 나무의 임의의 좌표(X, Y, Z)가 있을 때, 이미지가 맺히게 될 평면(가장 오른쪽 굵은 세로선)에서의 좌표를 (x, y, 1)이라고 할 때, normalized plane이라 함은 물체와 카메라의 거리가 Z라고 가정할 때, 카메라로부터 1미터 떨어진 거리에 모든 점을 projection 시켰을 때, 해당 평면 위에 어떤 위치에 어떻게 상이 맺힐지를 미터 단위로 표시하는 것을 말합니다. 여기서 1미터가 곧 depth를 의미하게 되는 것입니다. normalized plane은 1미터라는 기준점으로 약속된 정의로 보통 위처럼 물체의 맺힌 상을 표현할 때 사용하기 때문에 알아두는 것이 좋습니다. 그래서 이를 수식으로 표현하면 [X, Y, Z] = Z[u, v, 1]이 되는 것입니다.
그러나 우리는 이미지로 나타낼 것이기 때문에 미터를 또 픽셀 단위로 변환해 줘야 합니다. 아까 normalized plane은 3D를 2D로 바꾸는 작업이었다면, intrinsic parameter은 2D를 pixel로 바꿔주는 것입니다.
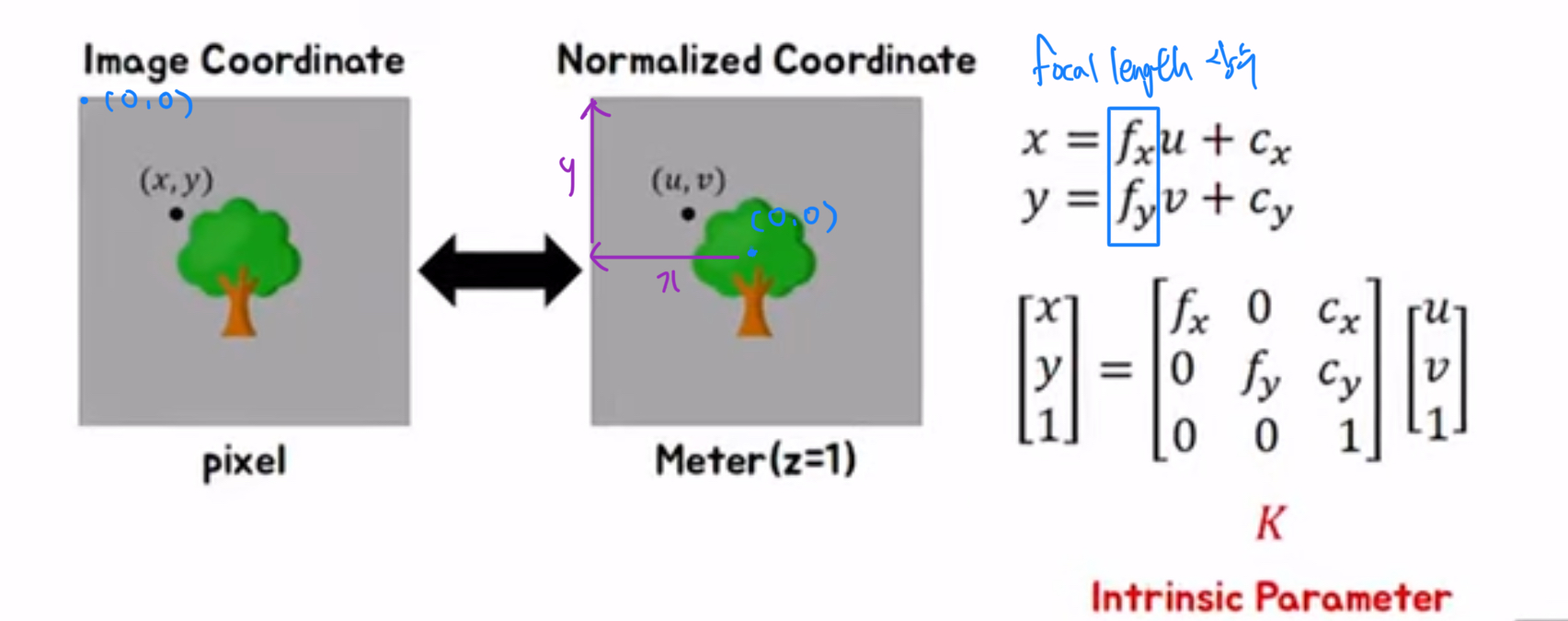
미터 단위를 픽셀로 변경해기 위해서는 먼저 x, y를 구해줘야 합니다. 먼저 f_x, f_y는 상수입니다. 이 상수는 몇 미터가 몇 픽셀에 해당하는지를 나타냅니다. 그리고 c_x, c_y는 중심점의 이동에 따른 오차라고 생각하면 됩니다. 위에 normalized plane의 사진을 봤을 때 우리는 카메라가 있는 초점은 (0, 0)으로 두고 나머지 좌표를 정의했습니다. 그러나 이미지에서는 사진처럼 왼쪽 위 꼭짓점을 중심으로 정의하게 됩니다. 그래서 보라색 화살표로 표시된 길이만큼 shifting을 시켜야 정확하게 픽셀 단위로 변환이 가능한 것입니다.
이 논문에서는 이 방법을 다루지는 않지만 이 parameter는 어떤 방식으로 픽셀 상으로 상을 맺히게 하는지를 간단하게 소개하는 부분입니다. 추가로 extrinsic parameter에서는 카메라가 회전함에 따라 얻을 수 있는 변환행렬을 곱하면 쉽게 변환된 시점의 이미지를 얻을 수 있다는 것을 보여줍니다.
본격 논문 리뷰
위에서 정립한 내용을 바탕으로 글을 보면 훨씬 간단함을 느낄 수 있습니다. 먼저 Introduction에서 말하고자 하는 것은 이 논문의 task입니다. 즉, 어떤 방식으로 view synthesis를 할 것인지 그 시나리오를 보여주는 것입니다.
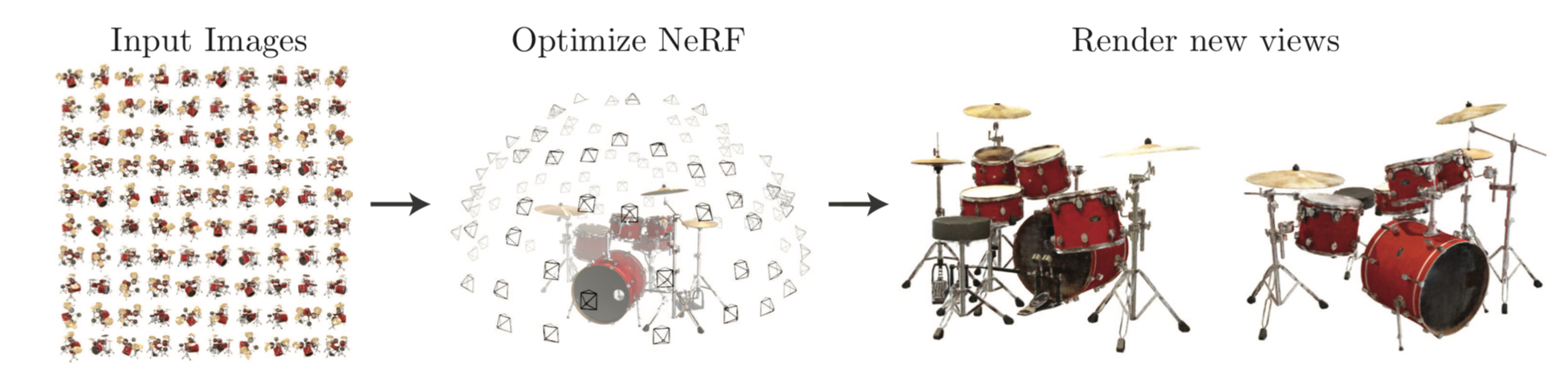
사진 왼쪽에 input 될 데이터가 존재합니다. 이 데이터는 물체를 N개의 시점에서 찍은 2D 이미지들입니다. 이를 통해서 얻고 싶은 건 우리가 삽입하지 않은 좌표에서 물체를 바라봤을 때의 view입니다. 가운데 사진을 보면 돔형으로 시점이 나오지만 완벽하게 빈틈이 없진 않습니다. 즉, 이 시나리오의 역할은 주어진 시점들로 저 빈 곳들을 예측하여 채워서 3D와 같이 만드는 것입니다. 정리하자면 N개의 시점에서의 이미지를 줬을 때, 임의의 좌표에서의 이미지를 얻는 것입니다. 그래서 보통은 정량평가 시, 100개의 이미지가 있다고 했을 때, 80개를 input 하고 도출된 나머지 20개를 실제로 찍은 20개와 얼마나 유사한지를 평가합니다.
Neural Radiance Field
그래서 도대체 NeRF가 무엇이냐? 요약하자면 NeRF는 view synthesis를 하기 위한, 3D로 렌더링 하기 위한 하나의 방법론입니다. 이미지는 각 위치에 pixel값을 저장한 하나의 테이블 형태입니다. 여기서 pixel값은 RGB의 값입니다. 그러나 만약에 3D로 표현한다면 테이블로 정의하는 것이 굉장히 힘들어집니다. 3D는 시작과 끝이 있는 것도 아니고, 사각형의 데이터로 표현하는 것이 어렵습니다. 그래서 이 논문에서 제시하는 방법인 NeRF(Neural Radiance Field)는 우리가 특정 위치값을 input으로 주면 output으로 해당 위치의 RGB값을 연산해 주는 함수입니다.
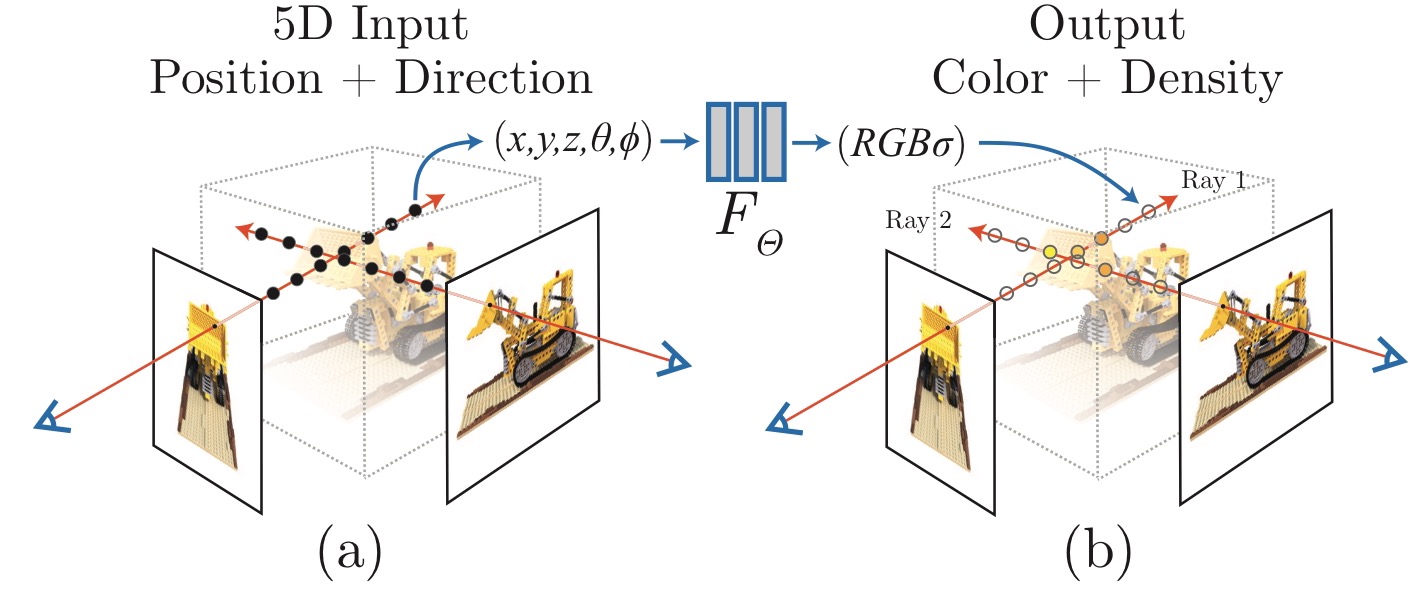
이러한 방식을 채택하게 되면 함수의 연산으로 3D 데이터를 통째로 모델링할 수 있게 됩니다. 그럼 이제 함수가 어떻게 이루어져 있는지 보겠습니다.
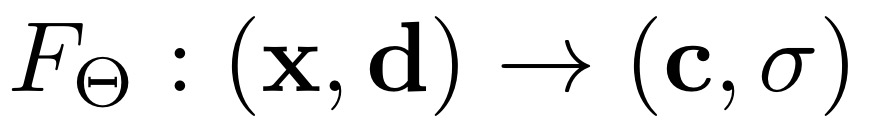
함수 F는 NeRF의 형태죠. 여기서 x와 c가 의미하는 것은 x라는 위치값을 입력했을 때, c라는 RGB값이 도출된다는 것입니다. x와 c는 위에서 말한 함수의 역할과 같지만 실제로는 d와 시그마를 설정합니다. d가 의미하는 것은 내가 물체를 바라보는 방향을 의미합니다. 이걸 input으로 넣는 이유는 보는 각도에 따라 RGB값이 바뀌는 경우가 있기 때문입니다. 예를 들어 밖에서 물체를 관찰한다고 할 때, 햇빛이나 그늘의 영향 등으로 어느 각도에서 바라보는지에 따라 상대적인 RGB값이 변할 것입니다. 그리고 d를 통해 나오는 시그마는 density를 의미합니다. density는 투명도의 역개념으로 해당 부분의 파티클의 밀도에 따라 얼마나 견고한 부분인지를 의미합니다. 쉽게 설명해서 창문 같이 뒤쪽이 관통하여 보이는 물체는 파티클의 밀도가 작다고 할 수 있기에 density가 작은 것, 벽과 같이 관통하여 보이지 않는 물체는 density가 높다는 것입니다.
추가적으로 이 논문에서 활용한 렌더링은 기존의 train과 test와 차이가 있습니다. 기존의 방법은 방대한 양의 데이터를 train으로 받아 학습을 시키고 test를 통해 예측을 하는 느낌이었습니다. 그러나 여기서는 zero shot super resolution처럼 train을 미리 하는 것이 아니라 test시에 input이 들어오면 그 input에 대해서만 학습을 새롭게 합니다.
Ray
Ray는 카메라에 상이 맺히게 됐을 때, 특정 위치의 RGB값에 영향을 준 모든 요소를 정의하는 직선입니다.
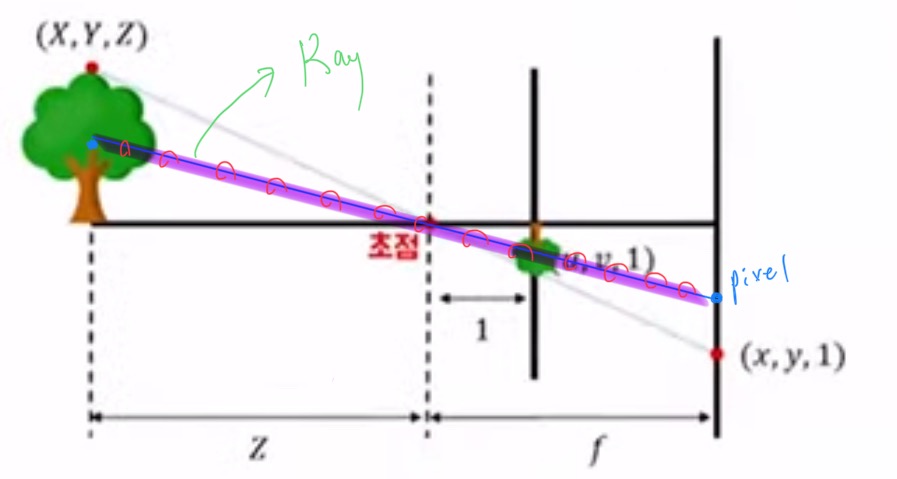
예를 들어 위 나무의 파란 점 부분을 위치로 설정해 보겠습니다. 원점이 카메라의 위치기 때문에 초점을 지나 상이 맺히는 부분에 특정 RGB값을 지닌 픽셀이 생성될 것입니다. 그러면 이 과정에서 직선을 하나 만들 수 있습니다. 수학적으로 직선이란 무수히 많은 점들로 이루어져 있습니다. 그렇다면 위 그림에서도 마찬가지로 직선 위에 있을 수많은 파티클 및 요소들이 pixel의 RGB값에 영향을 미친다는 것입니다. 예를 들어 나뭇잎은 초록색이지만 해당 직선에 위치할 햇빛의 영향을 받은 RGB값의 영향으로 살짝 연두색처럼 보일 수 있다는 것입니다.
여기서 해당 직선을 Ray라고 합니다. Ray를 수식으로 표현하면 초점 위치(o)로부터 어떤 방향(d)으로 t만큼 이동한 점들의 집합으로 o + td 라고 정의합니다.
Ray를 통해 projection 하는 방법은 간단합니다.
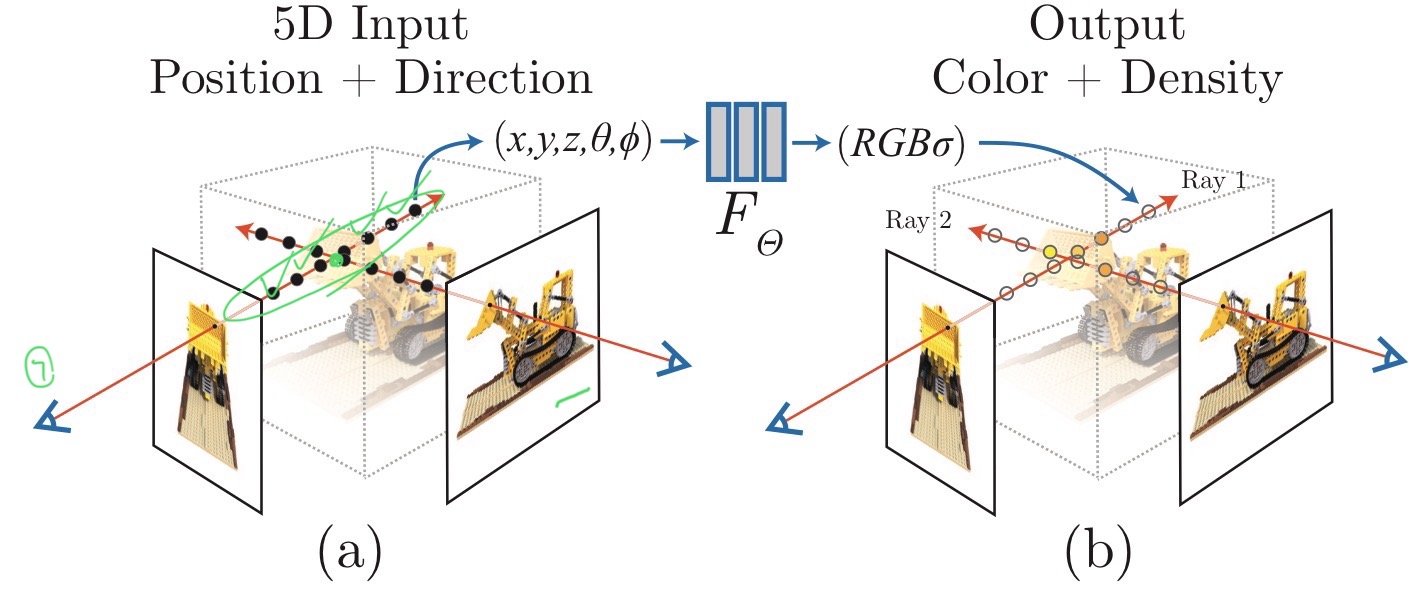
만약에 내가 ㄱ 시점에서 이미지를 정의하고 싶으면 모든 픽셀에 대한 Ray를 구하면 됩니다. 여기서 Ray를 구하는 방법은 카메라의 위치와 픽셀의 위치가 정해지면 두 점을 잇는 직선이 정의될 것이고 직선 위의 수많은 RGB값들 통해 픽셀의 RGB값이 정해질 것이고 렌더링이 진행될 것입니다.
그래서 결국 pixel값 = 한 Ray위에 존재하는 point들의 c값의 weighted sum이라고 표현할 수 있습니다. c값은 아까 말한 NeRF에서의 output인 RGB값입니다.
그럼 이제 우리는 이 weighted sum에서의 weight를 어떻게 처리할지를 생각해야 합니다. 이 상황에서 weight를 결정하는 가장 중요한 요소가 2개 있습니다.
1. Density가 클수록 Weight가 커야 한다.
2. 실제 위치 지점을 가로막고 있는 점들의 Density의 합이 작을수록 Weight가 커야 한다.
1번은 당연한 말입니다. Density가 크다는 것은 견고한 부분으로 해당 부분의 RGB값이 외부의 영향을 받지 않고 pixel값에 저장될 확률이 높습니다. 그렇기에 당연히 weight가 커야 하는 것이죠. 중요한 건 2번인데 2번이 의미하는 바는 내가 물체를 찍을 때 물체와 pixel 사이의 Ray의 점들의 Density의 합이 작을수록, 즉 물체와 pixel 사이에 가로막고 있는 게 없으면 없을수록 weight가 커야 한다는 것입니다. 예를 들어 제가 사람을 찍는데 카메라와 사람 사이에 벽이 있으면 사람이 나오지 않을 것입니다. 이유는 사람과 pixel을 잇는 Ray에서 사람과 pixel사이에 있는 점들의 Density가 너무 크기에 사람이 가리게 되는 것입니다. 그래서 사람과 카메라 사이에 벽이 없을수록, Density가 줄어들수록 사람이 잘 보이기 때문에 해당 지점은 Weight가 커야 합니다.
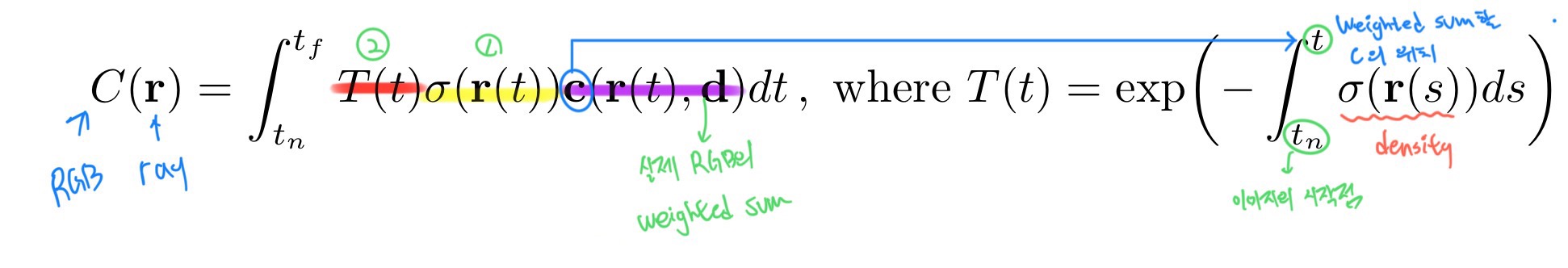
위 수식은 하나의 ray에 대해서 RGB값을 구하는 과정을 담았습니다. 보라색 부분은 실제 해당 지점의 RGB값의 weighted sum, 노란색 부분은 density를 나타내기에 2가지 요소 중 1번에 해당합니다. 빨간색 부분을 해석하면 이미지의 시작점, 즉 카메라부터 weighted sum을 할 c의 위치 요약하자면 물체와 초점 사이의 공간을 의미합니다. 이 공간에 대한 density를 적분하고 -를 붙이고 exp 해주는데 그 이유는 -후 exp를 해야 사이 공간의 density와 weight가 반비례하게 적용되기 때문입니다.
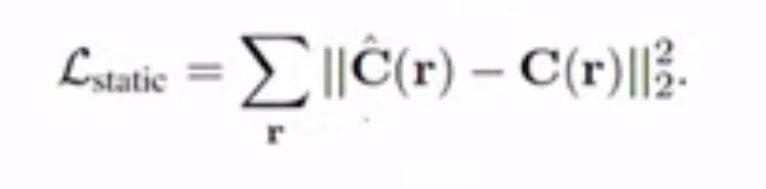
식을 살펴보면 빼주는 C(r)은 Ground-Truth값입니다. 왜냐하면 앞서 언급한 내용에서 view synthesis의 방식은 n개의 시점에서 찍은 이미지들을 주고 시작한다고 했습니다. 그래서 C(r)은 GT값이 되고 C_hat은 위의 C(r) 수식을 통해 도출되는 estimated value입니다. 우리는 density와 c값을 neural net을 이용한 FΘ로 도출할 수 있기 때문에 이를 estimated value로써 나타낼 수 있게 되는 것입니다. 그래서 이 두 가지 값의 차를 최소화하는 방향으로 학습을 시키는 것을 메커니즘으로 합니다.
Normalized Device Coordinates (NDC)
부연설명에 해당하는 부분입니다. NDC는 실제 세상의 물체를 cube space로 렌더링 하는 과정입니다. pinhole 카메라의 경우에는 초점부터 상이 맺히는 부분까지의 거리가 멀수록 더 크게 상이 맺힙니다. 그래서 보통 pinhole 카메라는 사각뿔의 형태로 이루어져 있습니다. 그럼 이를 일정한 길이의 cube 형태로 만들기 위해서는 좁았던 앞부분은 펴주고, 넓은 부분은 좁히는 과정이 필요합니다.
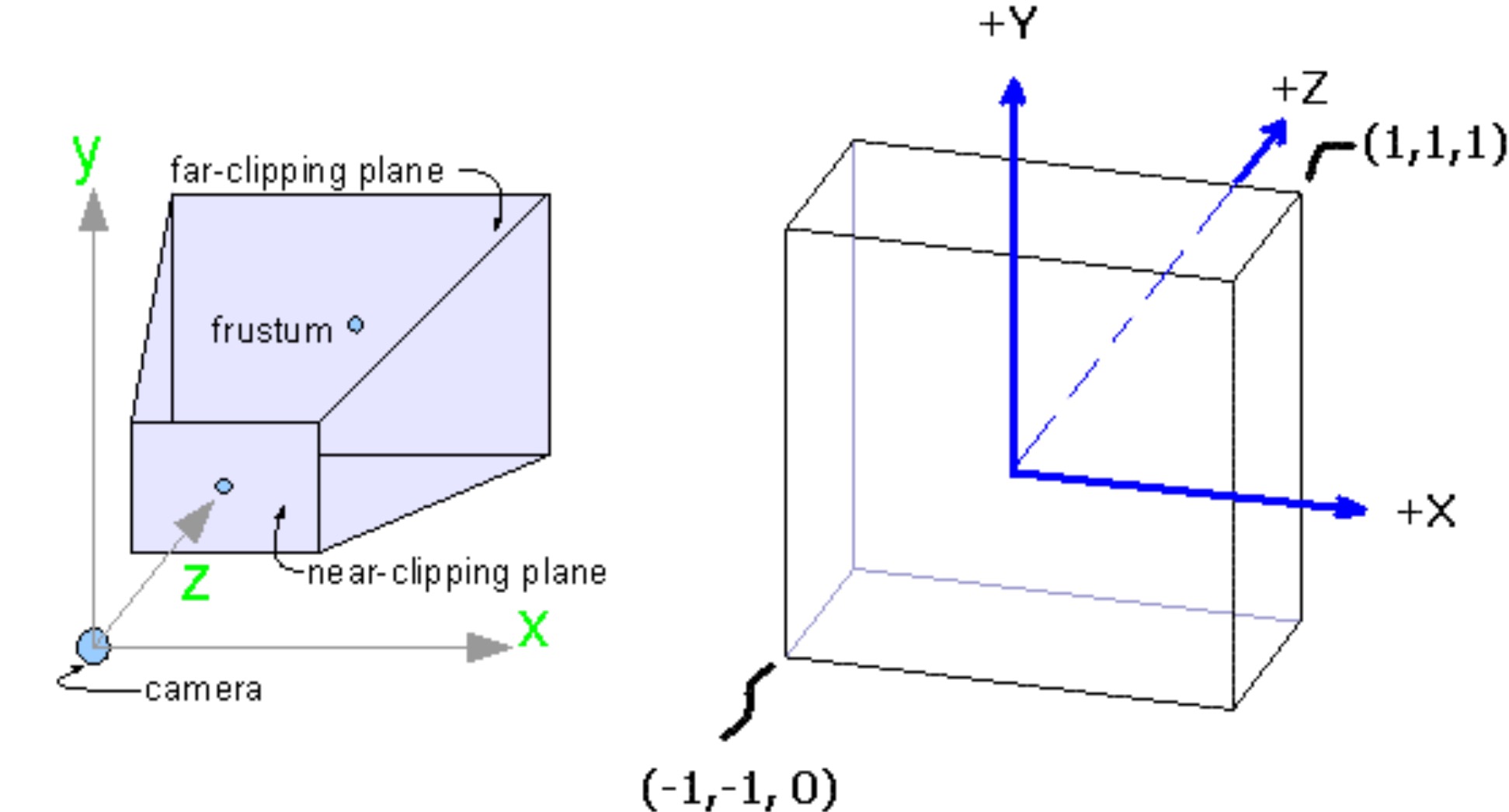
여기서 굳이 정육면체의 형태로 바꿔줘야 하는 이유는 NeRF자체가 원점인 (0, 0, 0)을 기준으로 -1부터 1까지 길이가 2인 필드에서 정의되는 체계를 가지고 있기 때문입니다. 그리고 위 사진에서의 정육면체 형태는 표준화된 좌표이고, 그래픽스 파이프라인(OpenGL, Direct3D 등)에서도 이를 이용하고 수학적 편의성을 챙기기 때문에 이러한 방식을 이용하는 거라고 생각하면 될 것 같습니다.

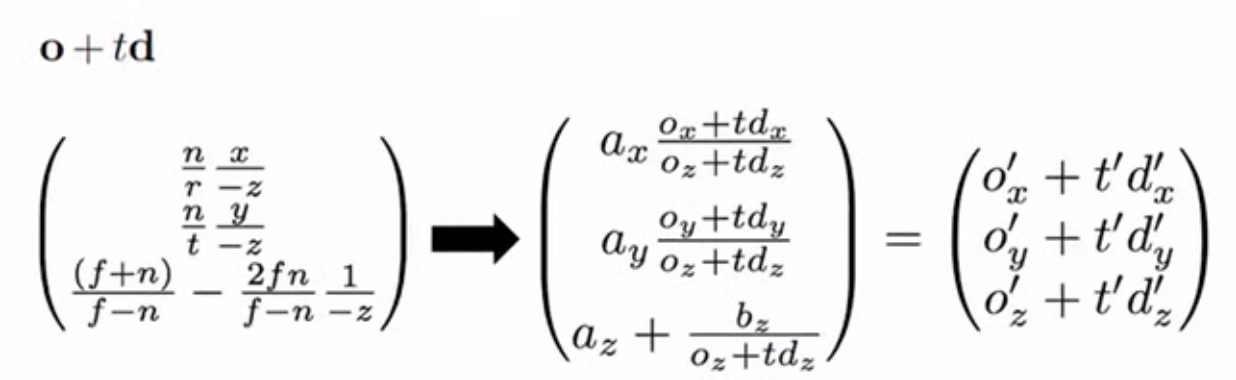
수식은 위와 같은데 특별히 중요하진 않고 뜻은 설명한 대로 좁은 부분은 늘리고, 넓은 부분은 줄여서 큐브 모양을 만드는 것입니다. 하지만 우리는 현재 ray를 정의해서 그 ray 위에 있는 점들을 적분하는 과정에서 c값을 얻으려고 하고 있습니다. 그러면 이제 o + td를 위 식에 적용하면 이제 기존의 좌표가 큐브 상으로는 어디에 해당하는지를 알 수 있을 것입니다. 아래의 식들로 해결할 수 있습니다.
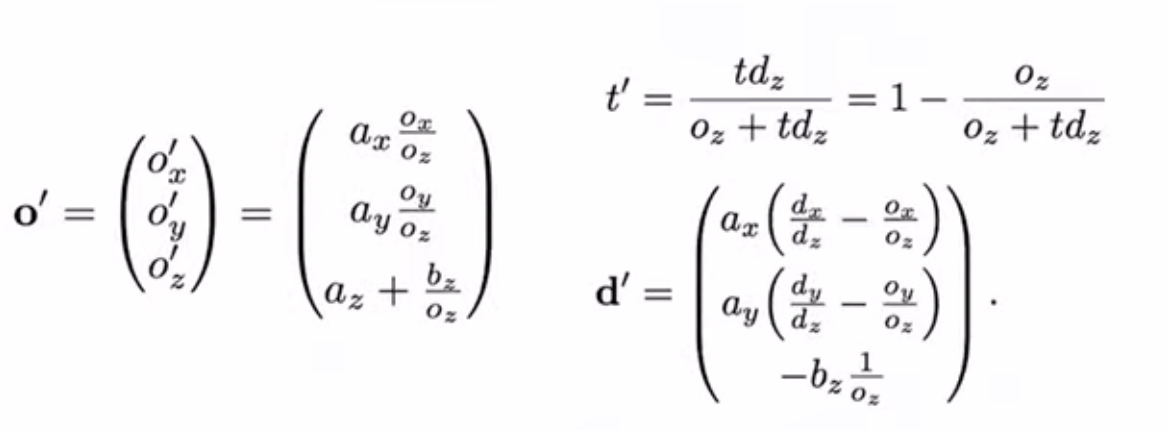
Implementation
이제는 위에서 랜더링 하는 것을 실제로 구현할 차례입니다. 앞서 구했던 C(r)은 t에 대하여 적분을 하는데 현실적으로는 ray에 있을 무한한 점들에 대해 모두 적분을 하는 것은 불가능합니다. 무한한 점들을 적분하는 것도 불가능하지만 물체와 카메라 사이가 대부분 공기라면 사이 공간에 대한 무분별한 적분은 굉장히 불필요한 작업이 됩니다. 그래서 t에 대해서 sampling을 진행합니다. 여기서는 이 기법을 stratified sampling approach(층화표집)이라고 부릅니다.
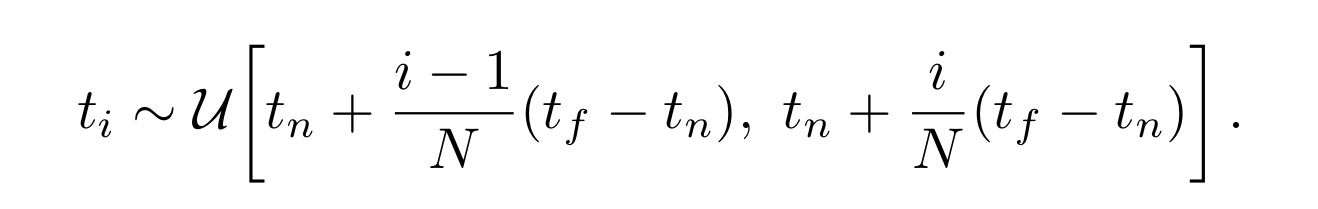
식은 거창하지만 뜻은 다음과 같습니다. ray가 있을 때 이를 n등분할 것입니다. 등분을 하게 되면 n개의 구간이 생기게 될 건데 이 안에 있는 점들 중 하나를 고르는 것입니다. 안에 있는 점들이 골라질 확률은 모두 같기 때문에 최종적으로는 매번 다른 패턴의 n개의 t가 적용될 것입니다.
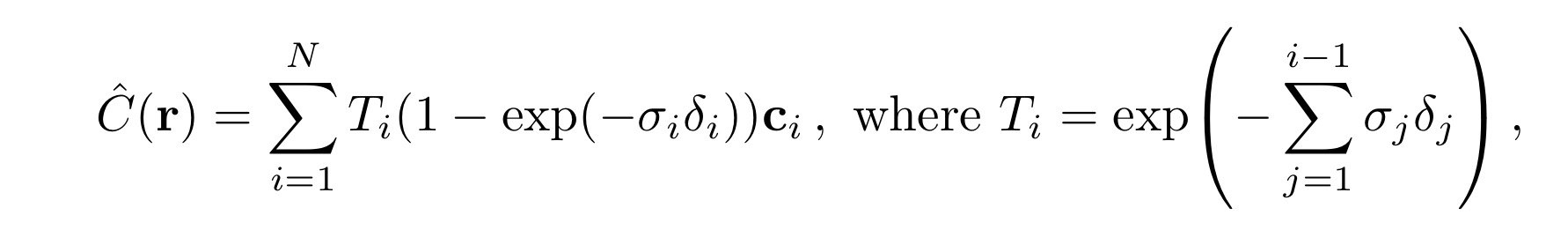
위 식은 앞서 나왔던 식과 유사하지만 세부적인 내용이 다릅니다. 특히 density에 해당하는 부분이 다른 것을 확인할 수 있습니다. 먼저 C(r)에서 T_i를 제외한 나머지 부분은 색상의 기여도에 대한 부분입니다. sigma_i는 density, delta_i는 흡수계수 라고 합니다. 흡수계수는 물질이 복사선을 흡수하는 정도를 나타내는 계수로 복사선의 파장에 따라 값이 달라진다고 합니다. 그리고 T_i에서 delta_j는 각 샘플 간의 거리를 뜻합니다.
이 모든 사항을 요약하면 이 식의 의미는 각 지점에서의 색상 기여도를 누적하여 최종 색상을 구하는 것입니다. T_i는 이전 지점까지의 투명도를 나타내고, ( (1 - \exp(-\sigma_i \delta_i)) )는 현재 지점에서의 흡수된 빛의 비율을 나타냅니다. 이를 통해 전체 광선의 색상이 결정됩니다. 따라서 식은 샘플링된 포인트에서의 색상과 투명도를 누적하여 광선의 최종 색상을 계산하는 방법을 나타내고 있습니다. 이는 연속적인 장면 표현을 위한 수치적 적분의 결과로 볼 수 있습니다.
하지만 저자는 위와 같은 방식이 굉장히 비효율적이라고 말합니다. 이유는 왜냐하면 ray가 통과하는 공간은 객체뿐만 아니라 아무것도 없는 공간도 포함되어 있기 때문이었죠. 별 도움이 안 되는 부분도 렌더링에 사용하니 좋은 결과가 나오기 힘들었던 것입니다. 그래서 생각해 낸 게 마지막 렌더링에서 예측되는 효과에 비례해 포인트를 sampling 하는 방식인 Hierarchical volume sampling이었습니다.
> Hierarchical volume sampling
1. Coarse Network 샘플링
첫 번째 단계에서는 coarse network를 사용하여 ray 상의 샘플들을 고르게 샘플링합니다. 이 샘플링은 전체 공간을 일정 간격으로 나누어 샘플을 추출합니다. 이 과정을 통해 coarse network가 대략적인 장면 구조를 학습하게 됩니다.
• Stratified Sampling: 광선을 일정한 간격으로 나누고 각 구간에서 무작위로 샘플을 추출합니다. 이는 각 구간에서의 샘플링 편향을 줄이고, 전체 광선에 대해 더 고르게 샘플을 분포시키기 위함입니다.
• Coarse Volume Rendering: coarse network는 이 샘플들로부터 밀도 및 색상 값을 예측하고, 이를 통해 초기 볼륨 렌더링 결과를 얻습니다.
2. Fine Network 샘플링
두 번째 단계에서는 fine network를 사용하여 첫 번째 단계에서 얻은 정보를 바탕으로 더 세밀한 샘플링을 수행합니다. 이는 중요한 영역에 대해 더 집중적인 샘플링을 수행하여 렌더링 품질을 높이는 역할을 합니다.
• Weighted Sampling: coarse network에서 얻은 결과를 바탕으로, 밀도가 높거나 중요한 디테일이 있을 가능성이 높은 영역을 더 집중적으로 샘플링합니다. 이를 위해, coarse network의 출력에 기반한 가중치를 사용하여 샘플링을 수행합니다.
• Importance Sampling: coarse network의 밀도 분포를 이용하여 중요한 영역에 더 많은 샘플을 할당합니다. 이는 실제 광선이 통과하는 경로에서 더 많은 샘플을 생성하여, 중 요한 디테일을 더 잘 포착할 수 있도록 합니다.
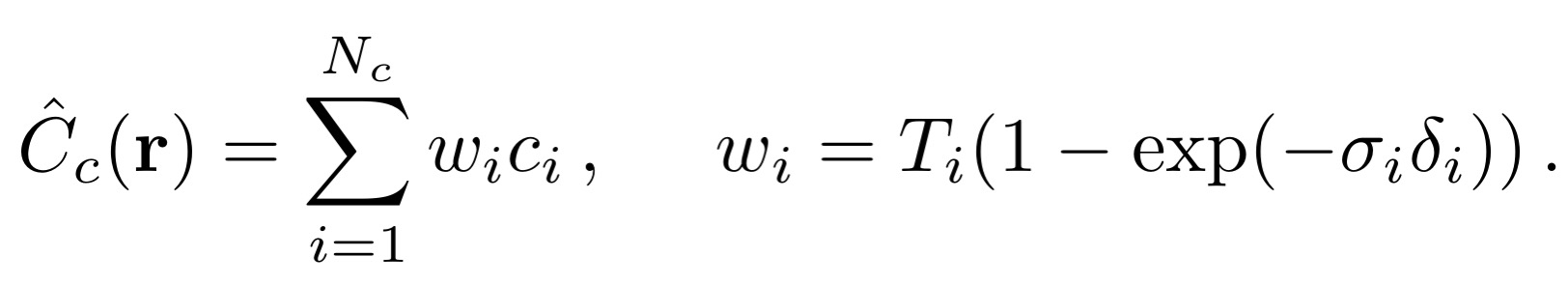
구체적인 절차
1. Coarse Sampling:
• 광선 ( r(t) )을 따라 ( N ) 개의 샘플 ( t_i )를 균등하게 추출합니다.
• 이 샘플들을 통해 coarse network에서 밀도와 색상을 예측합니다.
• 초기 볼륨 렌더링 결과 ( C_coarse(r) )를 계산합니다.
2. Fine Sampling:
• coarse network의 예측 밀도 값을 기반으로 더 세밀한 샘플링을 수행합니다.
• 예를 들어, coarse network에서 높은 밀도를 가진 영역에 더 많은 샘플을 집중적으로 할당합니다.
• 이 샘플들을 fine network에 입력하여 최종 밀도와 색상을 예측합니다.
• 최종 볼륨 렌더링 결과 ( C_fine(r) )를 계산합니다.
수식적 설명
1. Coarse Network 샘플링: 위에서 설명한 층화표집과 같습니다.
2. Fine Network 샘플링: coarse network의 결과를 바탕으로 중요 영역을 샘플링합니다. 이 과정은 밀도 분포를 기반으로 샘플링하는 가중치 ( w_i )를 이용합니다.
여기서 w_j는 coarse network에서 예측된 중요도에 기반한 가중치입니다.
> Positional Encoding
저자는 네트워크 F_Θ가 (x, y, z, θ, φ) 좌표를 바로 처리하였을 때 고주파 영역의 렌더링 성능이 크게 떨어진다는 것을 발견했습니다. 그리고 저자 외에도 다른 연구자가 이러한 현상을 발견했는데, 그는 네트워크가 저주파를 처리하는 함수로 학습되기 때문에 이러한 현상이 일어난다고 말했습니다. 즉, 현재 input 되는 데이터들의 차원은 총 6차원 좌표값 (x, y, z)와 방향 d에 대한 값 (x, y, z)를 넣는데 이는 neural net을 돌아 RGB와 sigma라는 4차원값을 뽑아내야 합니다. 그러나 6차원은 정보량이 너무 적기에 결과적으로 이미지가 선명하게 나오지 않는다고 합니다. 그래서 특정 식에 x, y, z 등을 넣어 차원을 뻥튀기시켜주는 것이 핵심입니다.
그리고 고주파 함수로 입력 데이터를 더 고차원 데이터로 매핑하고 네트워크에 입력값으로 넣으면 고주파 영역의 처리 성능이 향상된 방향으로 학습되는 것도 발견하였습니다.
저자는 이 점을 NeRF에 적용하였습니다. 그리고 네트워크 FΘ = F’Θ ◦ γ로 재구성하였을 때 성능이 매우 크게 향상된다는 점을 발견했습니다. 여기서 F’_Θ는 simply a regular MLP이며 γ는 R차원에서 R^(2L) 차원으로 매핑하는 함수이며 식을 자세히 적으면 다음과 같습니다.
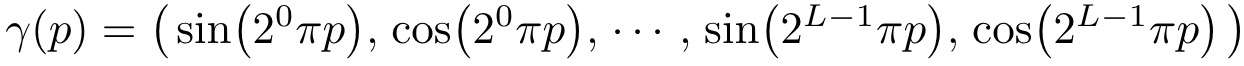
γ(·)는 입력 데이터 X = (x, y, z)의 각 원소 x, y, z와 X를 통과하는 camera ray의 unit vector d의 원소 x, y, z 모두 적용하여 해당 값들을 [-1, 1] 범위에서 normalize 합니다.
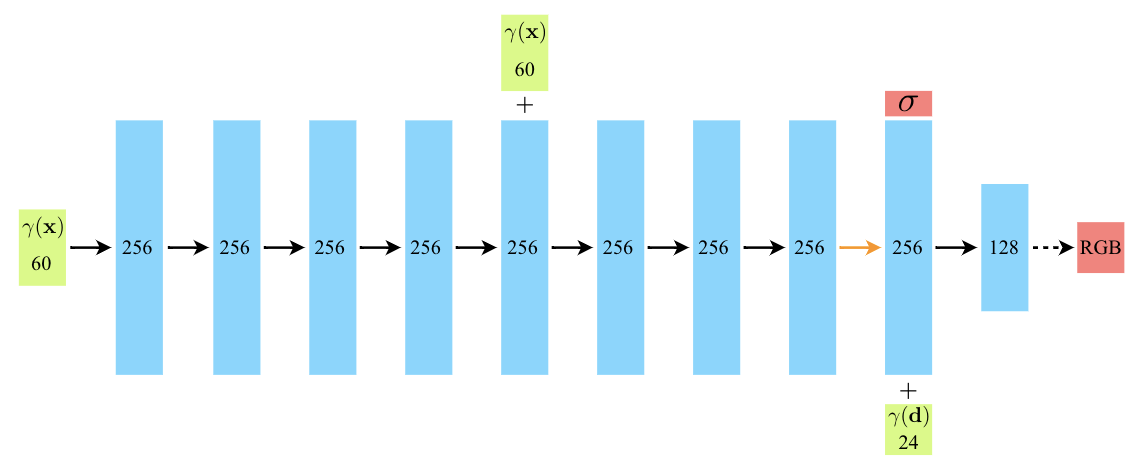
위는 실제 논문에서 사용한 neural network입니다. 여기서 layer들은 convolution이 아니라 FC layer들로 말 그대로 MLP입니다. 보게 되면 60차원짜리가 들어가서 쭉 가다가 정보 손실 방지 등을 이유로 60차원을 한 번 concat 해줍니다. 그리고 density를 뽑게 되는데 여기서는 보는 방향에 따라 density가 달라지지 않는다고 조건을 걸었습니다. 그래서 density를 뽑을 후 남은 feature vector에다가 d를 줘서 최종적으로 RGB를 얻게 되는 구조입니다.

그래서 보게 되면 positional encoding을 하지 않으면 선명도가 떨어지는 것을 알 수 있습니다.
여기까지 이 논문에 대해 알아봤습니다. 페이지 위의 링크에 들어가 보시면 다른 모델보다 확실히 좋은 성능을 내는 것을 확인할 수 있습니다. 그러나 NeRF의 진또배기는 바로 용량에 있다고 합니다. NeRF에서 사용하는 MLP의 parameter는 고작 5MB의 용량만 차지하며 15GB를 요구하는 LLFF와 비교했을 때 적말 적은 용량입니다.
후기…
음 처음으로 혼자 리뷰를 해봤는데 굉장히 어려웠습니다. 군대라는 공간에서 읽다 보니 오래 걸린 것도 있고, 검색이 원활하지 않고 코드도 읽기 힘든 환경이기 때문에 애를 먹었던 것 같습니다. 그리고 외부적인 요인을 제쳐두고 AI시장이 급변하는 상황에서 입대를 했기에 트렌드를 따라잡기 위해 기본적인 내용들을 숙지하려는 목적으로 읽었으나 아직 갈 길이 멀다는 것을 깨달았습니다. 자주 올리진 못하겠지만 최대한 시간이 나는 대로 열심히 해보겠습니다. 제가 잘 이해한 건지는 모르겠지만 읽어주셔서 감사합니다. ㅎㅎ
'군대시리즈 > Paper Review' 카테고리의 다른 글
| 논문 리뷰) Attention is all you need : 트랜스포머의 아키텍처 ② (1) | 2025.02.01 |
|---|---|
| 논문 리뷰) Attention is all you need : 트랜스포머의 아키텍처 ① (5) | 2025.01.23 |



댓글