합성곱 신경망에 대해 알아보겠습니다. 합성곱 신경망은 딥러닝을 하면서 많이 볼 수 있는 단어 중 하나인데 이토록 언급이 많이 되는 이유는 이미지 인식과 음성 인식 등에 사용되기 때문입니다.
합성곱 신경망의 전체적인 구조에 대해 살펴보면 이전과 유사함을 알 수 있습니다.
입력층 -> 합성곱층 -> 풀링층 -> 완전연결층 -> 출력층
위가 합성곱 신경망의 전체적인 구조인데 은닉층이 빠지고 그 자리에 새로운 계층들이 등장합니다.
이중 완전연결층은 이전에 다룬 Affine 계층이라는 이름으로 구현하였는데 Affine 계층은 완전연결층이라는 것이 걸맞게 인접하는 계층의 모든 뉴런들에 결합되어 있습니다.

이러한 사항들을 고려한다면 일반적인 신경망에서의 Affine 계층은 위와 같은 꼴을 하고 있을 것입니다.
그러나 합성곱 신경망에서는 합성곱층과 풀링층이 존재하기 때문에 형태가 다음과 같이 바뀝니다.

Conv가 합성곱층, Pooling이 풀링층입니다. 풀링층은 종종 생략되기도 합니다.
그렇다면 먼저 합성곱층에 대해 알아보겠습니다.
합성곱 계층
합성곱 신경망에서는 이전과는 새로운 단어들이 많이 등장합니다. 앞선 두 가지 그림에서 볼 수 있듯이 기존의 완전연결층과 합성곱 신경망에서의 완전연결층의 구조가 다른 것을 알 수 있습니다. 이는 기존의 완전연결층의 문제점을 보완하기 위함입니다.
완전연결층의 문제점이라고 한다면 데이터의 형상이 무시된다는 것입니다. 기본적으로 이미지 데이터의 경우에는 높이, 너비, 채널로 구성된 3차원 데이터입니다. 높이는 세로, 너비는 가로라고 불리기도 합니다. 채널은 색상으로 흑백사진인 그레이 스케일 사진은 채널이 1, 컬러는 채널이 3입니다.
예를 들어 MNIST 데이터의 경우에는 흑백이기 떄문에 채널이 1, 28x28이기 때문에 높이와 너비 모두 28입니다.
이를 코드 상에서 나타낼 땐 (1, 28, 28)처럼 나타낼 수 있습니다.
CNN에서는 합성곱 계층의 입출력 데이터를 특징 맵 또는 특성 맵이라고 부릅니다.
합성곱층에서는 입력되는 특징맵에 연산 과정을 거친 결과를 출력 특징 맵에 나타내는데 여기서 말하는 연산이 합성곱 연산입니다.
합성곱 연산은 우선 몇 가지 용어들이 등장합니다.
먼저 커널/필터입니다. 커널이나 필터 둘 중 아무렇게나 불러도 상관없습니다. 필터는 뭔가를 거른다는 느낌보다는 배치에 가깝게 생각하면 좋을 것 같습니다. 필터의 크기는 보통 3x3 아니면 5x5입니다. 필터는 고유한 크기를 가지고 있고, 각 칸에 특정 숫자가 적혀있습니다.
다음은 스트라이드입니다. 스트라이드는 영문을 해석하면 산책입니다. 보폭이라고 생각하면 편할 것 같습니다. 스트라이드는 1부터 시작해서 끝없이 큰 숫자를 대입할 수 있습니다. 스트라이드가 나타내는 보폭은 필터의 보폭입니다. 스트라이드가 1이라면 필터가 입력 데이터 위에서 1칸씩, 2면 2칸씩 이동합니다. 스트라이드는 풀링 계층에서도 중요하게 작용합니다.
위의 용어들을 바탕으로 합성곱 연산이 일어납니다.
일단 입력 데이터가 존재할 것입니다. 크기는 천차만별이겠지만 4x4로 가정해보겠습니다. 입력 데이터가 들어오게 되면 입력 데이터와 필터 사이에 합성곱 연산이 작용합니다. 필터가 3x3이라고 한다면 먼저 필터가 입력 데이터의 왼쪽 위에서 부터 단일 곱셈 누산 연산을 시작합니다.

위의 사진을 보면 아시겠지만 필터가 적용하는 영역 내에서 단일 곱셈 누산이 일어나 출력 특징 맵에 자리를 차지하게 됩니다. 그리고 스트라이드가 1이기 때문에 한 칸씩 움직인 것입니다. 물론 입력이 4x4라 스트라이드가 2가 될 수 없겠지만 입력의 크기가 더 크다면 스트라이드가 2일 때 2칸 씩 움직이게 될 것입니다. 만약 여기서 3의 편향이 작용한다고 하면 출력은 (18, 19, 9, 18)로 바뀔 것입니다.
그러나 보시다시피 필터 때문에 출력은 입력보다 크기가 작아질 수 밖에 없습니다. 만약 4x4의 입력을 4x4로 유지하고 싶거나 출력의 크기를 마음대로 조절하고 싶을 때 패딩을 사용합니다.

패딩이란 위의 입력 데이터와 같이 원하고자 하는 출력의 크기와 필터의 크기에 맞춰 빈 데이터로 감싸주는 것을 말합니다. 빈 데이터에는 0이 들어가는데 위처럼 4x4를 패딩으로 6x6을 만들면 출력의 크기가 줄어들지 않고 4x4로 유지됩니다.
사진은 채널이 1인 그레이 스케일 이미지였습니다. 그래서 데이터판과 같은 것이 하나 밖에 없었습니다. 그러면 컬러 사진일 때는 어떨까요? 컬러는 앞에서 말씀드렸다시피 채널이 3입니다. 채널이 3이기 때문에 입력 데이터의 형상이 예를 들어 4x4가 3개가 있는 형태가 될 것입니다.
여기서 주의해야할 점은 4x4짜리 판은 3개지만 이들은 모두 하나의 데이터라는 것입니다. 필터에도 이가 똑같이 적용됩니다. 4x4짜리 데이터 3개를 합성곱 연산하기 위해서는 하나의 필터가 사용되는 것이 아니라 필터의 채널도 채널의 개수와 맞게 사용됩니다. 필터가 3개인 것이 아닙니다. 필터의 채널이 3이 된 것입니다.
이를 그림으로 나타내면 다음과 같을 것입니다.

이 과정에서는 입력 데이터가 필터에 영향을 까친 사례라고 할 수 있습니다.
그렇다면 이번에는 만약에 필터 자체가 여러 개라면 어떻게 될까요?
답은 작용하는 필터의 개수가 특성 맵의 채널에 영향을 끼친다는 것입니다.
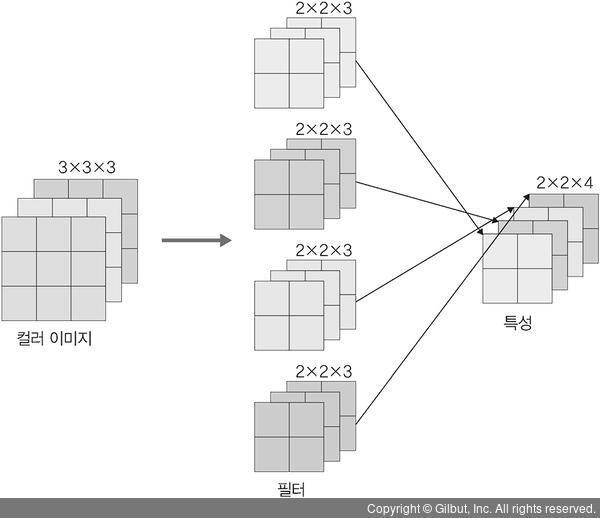
합성곱층에서의 연산을 정리하면 다음과 같습니다.
입력 데이터 : W1 x H1 x D1 (순서대로 가로, 세로, 채널)
<하이퍼 파라미터>
필터 개수 : K
필터 크기 : F
스트라이드 : S
패딩 : P
<출력 데이터>
· W2 = (W1 - F + 2P) / S + 1
· H2 = (H1 - F + 2P) / S + 1
· D2 = K
합성곱 연산은 배치 처리 또한 지원하는데 이는 각 계층을 흐르는 데이터의 차원을 하나 늘려 4차원의 데이터로 저장합니다. 구체적으로는 (데이터 수, 채널 수, 높이, 너비) 순으로 저장합니다.

각 데이터의 선두에 배치용 차원을 추가했습니다. 그리고 데이터는 4차원의 형상을 가진 채 각 계층을 타고 흐릅니다.
주의할 점은 신경망에 4차원 데이터가 하나 흐를 때마다 데이터 N개에 대한 합성곱 연산이 이뤄진다는 것입니다. 이 말은 즉, N회 분의 처리를 한 번에 수행하는 것입니다.
이상으로 합성곱 신경망 CNN에서의 합성곱 계층에 대해 알아봤습니다.
'AI > Deep learning from Scratch' 카테고리의 다른 글
| [머신러닝, 딥러닝] 합성곱 신경망 (3) (0) | 2023.03.01 |
|---|---|
| [머신러닝, 딥러닝] 합성곱 신경망 (2) (0) | 2023.03.01 |
| [머신러닝, 딥러닝] 오차역전파법 (3) - 오차역전파법 구현 (0) | 2023.02.15 |
| [머신러닝, 딥러닝] 오차역전파법 (2) - 계층 (0) | 2023.02.15 |
| [머신러닝, 딥러닝] 오차역전파법 (1) - 역전파와 계산법칙 (0) | 2023.02.14 |




댓글