이전 페이지에서 합성곱 신경망의 전체적인 구조와 그중 합성곱층에 대해 소개를 했습니다.
이번에는 다음 층인 풀링층부터 알아보도록 하겠습니다.
풀링 계층
풀링층이 하는 역할은 간단합니다. 바로 이미지를 축소시키는 것입니다.
풀링층은 특성 맵의 차원을 다운 샘플링하여 연산량을 감소시키고, 주요한 특성 벡터를 추출하여 학습을 효과적으로 할 수 있게 합니다. 다운 샘플링이란 이미지를 축소시키는 것을 의미합니다.
풀링 연산에는 두 가지가 사용되는데 최대 풀링과 평균 풀링이 있습니다.
최대 풀링은 최댓값을 추출하는 것이고 평균 풀링은 평균을 반환하는 것입니다.

위 사진이 최대 풀링을 하는 과정입니다. 두 칸 씩 이동하기 때문에 스트라이드는 2인 것을 알 수 있습니다.
간단하게 평균 풀링도 계산해보시면 알겠지만 도출되는 값이 살짝 다르다는 것을 알 수 있습니다.
여기서 얻을 수 있는 결과는 두 가지 과정 모두 계산 과정은 다르지만 사용하는 파라미터는 동일하다는 것입니다.
《위에서는 2x2의 영역으로 풀링을 진행하였습니다. 여기서 말하는 영역이 스트라이드를 정하는 기준이 됩니다.
앞선 내용에서 합성곱층에서는 스트라이드를 1로 설정하여 데이터들을 겹치게 연산하는 것이 일반적이었습니다. 그러나 풀링층에서는 데이터가 서로 겹치지 않게 스트라이드를 설정합니다. 그 이유가 무엇일까요?
- 그것은 각 계층이 하는 역할이 다르기 때문입니다. 합성곱층이 하는 역할은 데이터의 특성을 추출하는 역할입니다. 그래서 저희는 필터와 특성맵이라는 개념을 활용하여 연산을 했습니다. 특성을 추출하는데 필요한 것이 바로 데이터의 위치입니다. 필터는 데이터 전체를 훑으면서 지나갑니다. 원래는 겹치는 영역을 두지 않는 게 좋을 수 있지만 스트라이드를 1로 두고 필터가 훑게 되면 중간에 빠지는 연결고리 없이 모든 데이터 간의 관계를 훑으며 특성을 추출할 수 있기 때문에 결과에 지장이 생기지 않는다는 것입니다.
그러나 이를 만약 풀링층에 적용하게 되면 문제가 생깁니다. 풀링층의 가장 큰 목적은 원본과 가장 유사하게 축소시키는 것입니다. 예를 들어 4x4의 데이터를 2x2로 풀링하는데 스트라이드가 1이라면 만약 4x4의 중간쯤에 6처럼 압도적으로 큰 숫자가 있을 때 스트라이드가 1이 되어버리면 최대 풀링을 할 때 그 주변은 모두 6으로 일반화가 됩니다. 그러면 원본 사진에 비해 많이 다르게 될 것입니다.
그래서 결과적으로 말하자면 합성곱층은 모든 데이터 간에 연결을 보는 것을 중시하기 때문에 스트라이드를 작게 설정해 특성을 정확하게 추출하는 것은 상관이 없, 풀링층은 원본과의 정확성을 유지시키기 위해 겹치는 데이터 없이 전체를 분할하여 각각의 특성을 정확하게 내보내야 하기에 전체 데이터를 나누는 분할에 맞는 스트라이드를 설정해야 한다는 것입니다.》
풀링층의 특징이라고 한다면 합습해야할 매개변수가 없고, 채널 수가 변하지 않고, 입력 데이터의 변화에 영향을 적게 받는 것이 있습니다.
풀링층도 합성곱층과 같이 정리하면 다음과 같습니다.
입력 데이터 : W1 x H1 x D1 (순서대로 가로, 세로, 채널)
<하이퍼 파라미터>
필터 크기 : F
스트라이드 : S
<출력 데이터>
· W2 = (W1 - F) / S + 1
· H2 = (H1 - F) / S + 1
· D2 = D1
그럼 이제 합성곱층과 풀링층을 구현할 차례입니다.
먼저 무작위 4차원 배열을 만들어보겠습니다.
import numpy as np
# 무작위 4차원 배열 만들기
x = np.random.rand(10, 1, 28, 28)넘파이를 이용하면 위와 같이 쉽게 만들 수 있습니다.
그다음은 이제 합성곱 연산을 구현해야 하는데 원래대로라면 for문을 겹겹이 쓰면서 코드가 복잡해지겠죠.
이러한 문제점 때문에 im2col이라는 편의 함수를 사용합니다. im2col이 하는 일은 3차원의 입력 데이터를 2차원으로 변환하는 역할을 합니다. 2차원으로 펼치면 필터가 일을 하기 수월해지겠죠? 해당 전개를 필터가 적용되는 모든 영역에 수행하는 것이 im2col입니다.
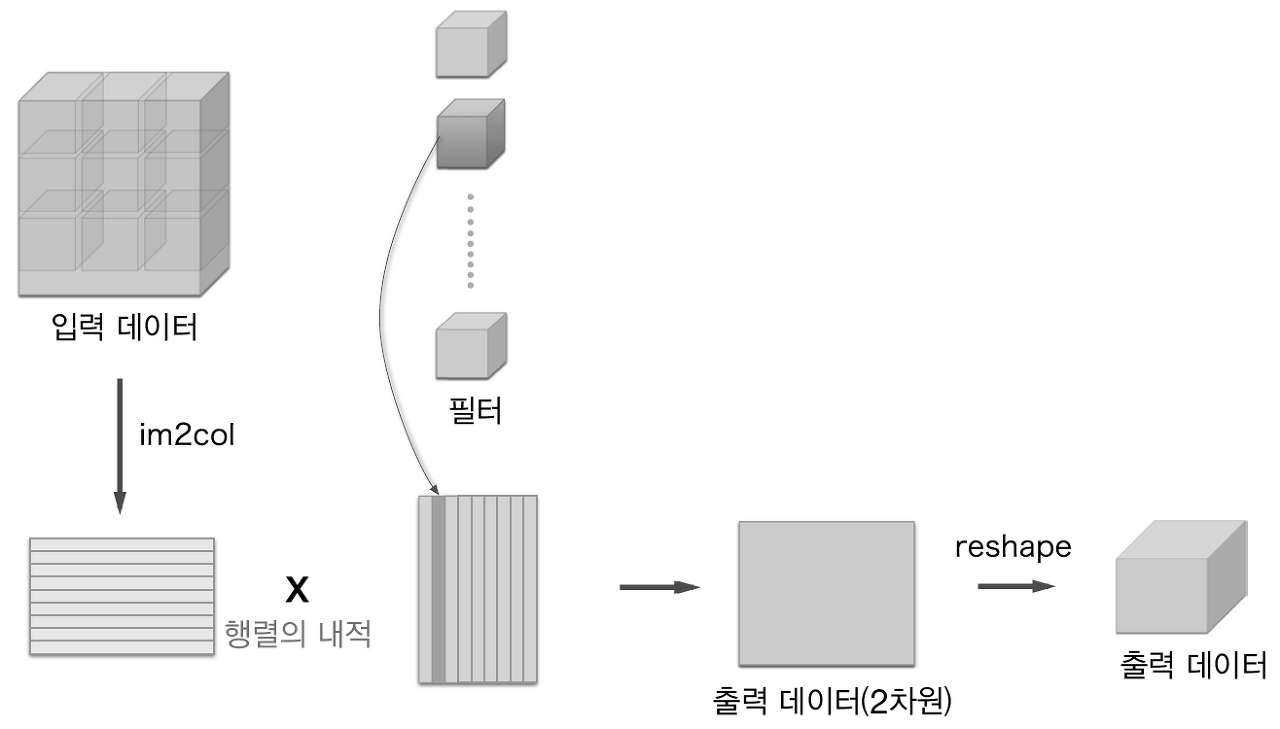
그림처럼 입력 데이터를 2차원으로 변형시키고 연산을 모두 수행한 후 다시 원래 형태로 reshape 시켜야합니다.
im2col부터 구현하면 다음과 같습니다.
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
"""다수의 이미지를 입력받아 2차원 배열로 변환한다(평탄화).
Parameters
----------
input_data : 4차원 배열 형태의 입력 데이터(이미지 수, 채널 수, 높이, 너비)
filter_h : 필터의 높이
filter_w : 필터의 너비
stride : 스트라이드
pad : 패딩
Returns
-------
col : 2차원 배열
"""
N, C, H, W = input_data.shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
return col위에서 out_h와 out_w에서 이전에 작성한 출력 데이터의 식을 찾아볼 수 있습니다. 그리고 밑에 for문을 통해서 2차원으로 reshape 합니다.
이를 활용해 보면 다음과 같습니다.
from util import im2col
x1 = np.random.rand(1,3,7,7)
col1 = im2col(x1, 5, 5, stride=1, pad=0)
print(col1.shape)
x2 = np.random.rand(10, 3, 7, 7)
col2 = im2col(x2, 5, 5, stride=1, pad=0)
print(col2.shape)다음은 합성곱 계층을 구현한 것입니다.
# 합성곱 계층 구현
class Convolution:
def __init__(self, W, b, stride=1, pad=0):
self.W=W
self.b=b
self.stride=stride
self.pad=pad
def forward(self, x):
FN, C, FH, FW = self.W.shape # 필터 개수, 채널, 필터 높이, 필터 너비
N, C, H, W = x.shape
out_h = int(1 + (H + 2*self.pad - FH) / self.stride)
out_w = int(1 + (W + 2*self.pad - FW) / self.stride)
col = im2col(x, FH, FW, self.stride, self.pad)
col_w = self.w.reshape(FN, -1).T # 필터 전개개
out = np.dot(col, col_w) + self.b
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
return out위 코드의 흐름은 다음과 같습니다.
1. 합성곱 계층에서 init에서 W, b, S, P를 받아옵니다.
2. forward에서 input에서 filter을 통해 output을 계산해야 합니다.
3. W의 shape을 (FN, C, FH, FW)으로, x의 shape을 (N, C, H, W)으로 만들고 out_h, out_w도 공식을 통해 계산합니다.
4. col은 input을 im2col로 펼친 2차원 데이터, col_W은 W의 필터들을 열로 펼친 2차원 데이터입니다.
5. col은 im2col로 처리해 주고, col_W는 FN이 열 수가 되도록 reshape 합니다.
6. output은 col과 col_W의 행렬곱에 편향인 b를 더한 것입니다.
7. 이때 out은 3차원이고 이를 4차원 데이터로 reshape 해줍니다.
8. transpose는 다차원 배열의 축 순서를 바꿔주는 함수입니다.
그리고 reshape에서 -1 같은 경우에는 다차원 배열의 원소 수가 변환 후에도 똑같이 유지되도록 적절히 묶어주는 편의 기능입니다.
다음은 풀링 계층의 구현입니다.
풀링층에서의 다른 점은 채널에 독립적이라는 것입니다.

풀링층의 구현 흐름은 다음과 같습니다.
풀링 적용 영역을 채널마다 다르게 처리해야 합니다. 입력 데이터에서 채널들을 전개하고, 풀링 적용 영역을 행으로 길게 만들고, 행별로 최댓값을 뽑아서 다시 reshape 합니다.
- 입력 데이터를 전개한다
- 행별 최댓값을 구한다
- 적절한 모양으로 reshape 한다.
위의 내용들을 구현하면 다음과 같습니다.
class Pooling:
def __init__(self, pool_h, pool_w, stride=1, pad=0):
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
def forward(self, x):
N, C, H, W = x.shape
out_h = int(1 + (H - self.pool_h) / self.stride)
out_w = int(1 + (W - self.pool_w) / self.stride)
# 전개
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
col = col.reshape(-1, self.pool_h * self.pool_w)
# 최댓값 axis : 축의 방향, 0=열방향, 1=행방향
out = np.max(col, axis=1)
# 성형
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
return out코드의 흐름은 다음과 같습니다.
1. init에서 pooling 영역이 지정될 FH, FW, S, P를 입력받습니다.
2. forward에서 (N, C, H, W)로 x의 shape을 잡고, out_h, out_w를 계산합니다. im2col으로 col을 전개해줍니다. PH*PW가 열 수가 되도록 reshape 해줍니다.
3. col의 행 별 최댓값을 찾아준 뒤 4차원이 되도록 reshape 해줍니다.
이상으로 합성곱 신경망에서 합성곱 계층과 풀링 계층의 구현을 im2col 함수와 함께 알아봤습니다.
'AI > Deep learning from Scratch' 카테고리의 다른 글
| [머신러닝, 딥러닝] 합성곱 신경망 (3) (0) | 2023.03.01 |
|---|---|
| [머신러닝, 딥러닝] 합성곱 신경망 (1) (1) | 2023.03.01 |
| [머신러닝, 딥러닝] 오차역전파법 (3) - 오차역전파법 구현 (0) | 2023.02.15 |
| [머신러닝, 딥러닝] 오차역전파법 (2) - 계층 (0) | 2023.02.15 |
| [머신러닝, 딥러닝] 오차역전파법 (1) - 역전파와 계산법칙 (0) | 2023.02.14 |




댓글